단순선형회귀 이론과 파이썬 예제코드

1. Intro

 

데이터사이언스를 크게 나누면 지도학습/ 비지도학습 (답이 정해져있냐 아니냐) 로 나뉜다. 지도학습은 그 안에서도 보통 (예측, 분류, 강화) 요렇게 세 그룹으로 나뉘는데 이 중에서도 예측, 그리고 뭔가 일반적인 패턴에서 벗어난 이상치에 대한 "이상 검출" 은 통계와 엄청 밀접한 관계가 있다고 함! 

 

 

2. 단순선형회귀 

 

단순선형회귀는 선형회귀모델 중에서도 가장 초 심플한 함수 형태의 모델이다. X 가 증가 혹은 감소함에 따라 Y 는 어떻게 되는지를 보여주는,, 방법이지! 이 방법을 쓰면 두 변수 사이의 관계를 정량화해 나타낼 수 있음 

 

너무 당연한 회귀곡선의 식.. 1차방정식 !

 

 

중 1 때 우리가 배웠던 1차방정식.. 요것이 단순회귀식이다. 

 

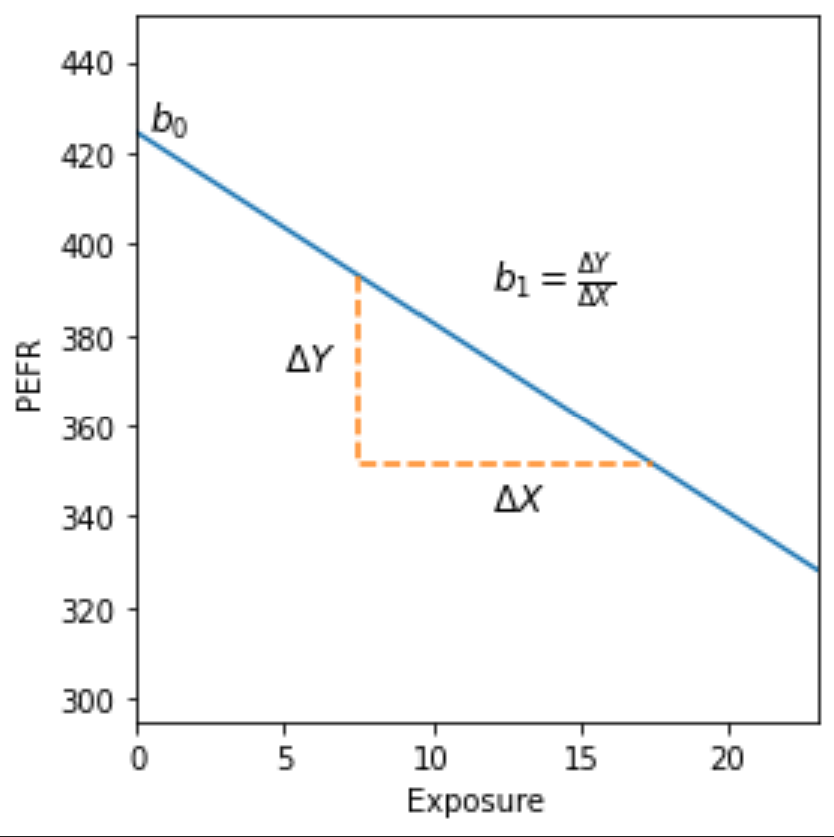
우리가 이때 구해야 하는 것들은 b1 (기울기) 와 b0 (절편) 이다. 그걸 알면 X 에 따라 Y 가 어떻게 바뀌는지 알 수 있지요.. 이때 X 는 독립변수 (안 바뀌니까요) Y 는 종속변수 (X 에 따라 바뀌니까요) 이렇게 부르는데 데이터 분야에서는 각각 featur 와 target 이라고 부른다. 

 

예시를 들자면..! 이 그래프는 노동자들이 면진에 노출된 연수와 폐활량의 상관관계를 그린거다. 이 각각 데이터들의 관계의 패턴을 파악해서 절편과 기울기를 알아내 함수를 완성하는게 우리가 할 일이지 

 

 

근데 저 산점도만 봐서 패턴이 보이세요? 일단 전 안보임...ㅎㅎㅎ 고것은 파이썬이 구해다 줄거다 

피쳐와 타깃을 지정해주고 선형회귀를 선언, 학습을 시켜주면 파라미터로 기울기와 회귀계수를 알 수 있다 

 

predictors = ['Exposure']
outcome = 'PEFR'

model = LinearRegression()
model.fit(lung[predictors], lung[outcome])

print(f'Intercept: {model.intercept_:.3f}') #기울기
print(f'Coefficient Exposure: {model.coef_[0]:.3f}') #회귀계수

Intercept: 424.583
Coefficient Exposure: -4.185

 

시각화 

 

 

자 이게 파이썬이 우리에게 구해다준 단순회귀 모델이다

 

근데 저 방식으로 예측을 하는건 상당히 별로인 방식일 수 있다 

 

 

왜냐면 아까 전에 본 산점도와 저 직선 사이의 오차가 상당하기 때문이다 (한눈에 봐도) ... 요걸 잔차residuals 라고 하는데 원래의 값에서 모델이 예측해준 값 (직선 위의 값) 을 빼면 그 잔차를 구할 수 있다 

 

fitted = model.predict(lung[predictors])
residuals = lung[outcome] - fitted

 

주황 선은 실제값과 예측값 사이의 잔차를 보여준다 

 

 

 

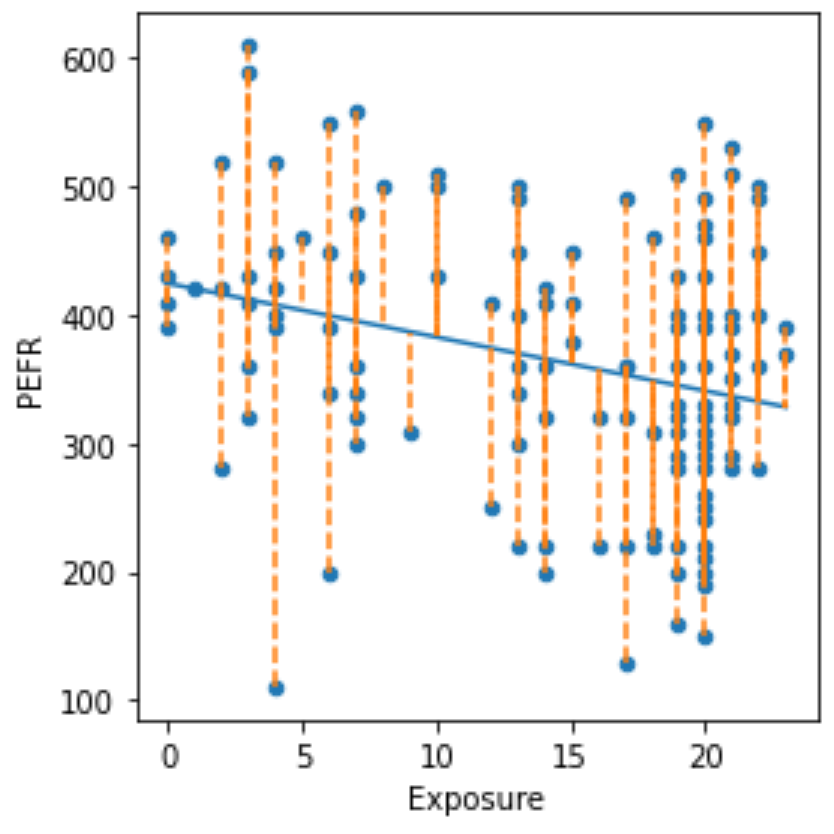
자 그럼 이제 저 잔차를 가장 줄이려면 우리 뭘 해야할까? 저 선의 기울기나 미세한 위치에 따라 잔차가 가장 적은 곳을 찾으면 된다! 고걸 하는 방법을 "최소제곱회귀" 라고 부른다. 구체적인 방법은 여기로 이동! Statquest 를 보고 적었다

 

https://blog.naver.com/didpql533/222712997644

[이론] 단순회귀

 

 

 

 

3. 회귀의 활용

 

일반적으로 데이터 사이언스에서 부르는 회귀는 위와같은 선형회귀다. 다음 챕터에서 다중선형회귀 (예측변수가 여러개인 경우) 도 다룰건데, 보통의 경우 타깃에 대한 변수는 보통 여러개이기 때문에 다중선형회귀를 쓰는 게 조금 더 일반적인 경우같다. 

 

회귀는 이렇게 예측을 하는데도 쓸 수 있고 , DA 적 관점에서 보면 데이터 간의 관계를 "설명" 하는 용으로도 쓸 수 있는 것 같음!